Twice-Multilayered Neural Nets (TMNN)

Since fundamental McCulloch and Pitts work (1943) neurons are considered as the binary, two or three equilibriums states components of neuronet. We can use the GMDH algorith]ms not as binary, but as complex neurons, where the self-organization processes are well studied. In the neuronet with such neurons, we shall have twofold multilayered structure: neurons themselves are multilayered, and they will be united into common matrix in multilayered way. GMDH algorithms are the examples of complex active neurons, because they choose the effective inputs and corresponding coefficients by themselves, in process of self-organization. The problem of neuronet links structure self-organization is solved in a rather simple way [9,10,30,34].

Each neuron is an elementary system that handles the same task. The objective sought in combining many neurons into a network is to enhance the accuracy in achieving the assigned task through a better use of input data. In the self-organization of a neural network, the exhaustive search is first applied to determine the number of neuron layers and the sets of input and output variables for each neuron. The minimum of the discriminating criterion suggests the variables for which it is advantageous to build a neural network and how many neuronet layers should be used.

Active neurons are able, during the self-organizing process, to estimate which inputs are necessary to minimise the given objective function of the neuron. They can provide generation of new very effective features of special type (the outputs of neurons from previous layer) and the choice of effective set of factors at each layer of neurons. Number of active neurons in each layer is equal to number of variables given in initial data sampling. First layer of active neurons acts similar to Kalman filter: output set of variables repeated the input set but with filtration of noises.

In another words, neuronet can be described as matrix, which unites active neurons in several layers. The neurons of each layer differs one from another by their output and input sets of variables. The output variables of each layer of active neurons are used as the input variables for next layer. Extension of regression area always can only perfect the result of regression. In the neuronet, considered below, extension is realized by very special way. For example, if the first layer of active neurons obtains set of input variables x₁,x₂,...,x_M and generates the set of output variables y ₁, y₂, ..., y_L , then the neurons of second layer obtains the both set of variables on its input. Extension of variables set always is accompanied by reasonable narrowing of variables number by criterion to prevent the exceed of computer ability (for allowed computer calculation time). It is possible to compare different schemes of data sample extension or narrowing by external criterion value.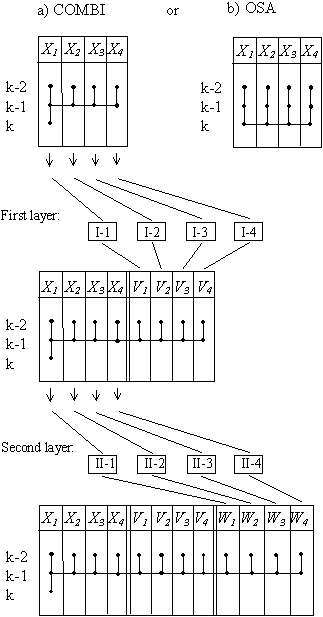

To begin with, we construct the first layer of neurons in the network. Then we will able to determine how accurate the forecast will be for all variables. For this purpose, we use a discrete template that allows a delay of one or two days for all variables. Calculated values of forecasts for all variables form additional subsample of variables. Then we add a second, a third, etc. layer to the neural network, as shown in figure, and go on doing so as long as this improves the forecast or decrease external criterion value. For each neuron, we have applied the extended definition procedure to one model. It may be inferred, that there is no need to construct a neural network in order to form a forecast for that variables, for which variation criterion value takes on the least value in the first layer. It is advisable to use a neural network to form a forecast for the variables, for which the variation criterion takes on the least value in the last layers of neurons. The sorting characteristic "number of neuronet layers - external criterion value" - defines the optimum number of layers for each variable separately.

Not only GMDH algorithms, but many modeling or pattern recognition algorithms can be used as active neurons. Its accuracy can be increased in two ways:

• each output of algorithm (active neuron) generate new variable which can be used as a new factor in next layers of neuronet;
• the set of factors can be optimized at each layer. The factors (including new generated) can be ranked after their efficiency and several of the most efficient factors can be used as inputs for next layers of neurons. In usual once-multilayered NN the set of input variables can be chosen once only.

Neuronets with active neurons should be applied to raise the accuracy of modeling and pattern recognition algorithms. As example, the forecast of New York Stock Exchange activity indexes is presented.