Extended definition of the optimal model
    by the theory of discriminating criteria

It has been demonstrated theoretically and experimentally that the exhaustive-search curves are gradual and unimodal for the expected value of the criterion [25]. The number of candidate models tested in each exhaustive-search layer cannot be infinitely large. Because of this, the curves take on a slightly wavy shape, and a small error may creep into the optimal model structure choice.

Therefore almost every GMDH algorithm consecutively uses two criteria. At first, an exhaustive search is applied to all candidate models for compliance with the main criterion, and a small number of models whose structure is close to optimal is selected. Then only one optimal model is selected that complies with a special discriminating criterion. The forecast error variation criterion RR(s) is proposed [15]:

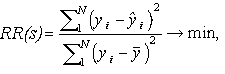
RR(s) = ( SUM(yi - yi^ )^2) / SUM(yi - y~)^2)
where: yi - is the variable value in the input data sample;   yi^ - is the variable value calculated according to the model and y~ is the mean value of variable or the value of trend function.

The majority of criteria of structure quality of model is separate case of general formulae [24]:

CR(s,n,X,y) = h1(s,n)V(s,n,X,y) + h2(s,n)D2,

where V(.) - magnitude of model error;
    h1(.), h2(.) - multiplicative and additive fine functions for model complexity (limit growth of estimated parameters number);
    D2 - estimation of unknown dispersion d2.

Compromise between model accuracy and its complexity typical for criteria of structural identification can be expressed explicitly or implicitly. For external criteria implicit fine is reached by division of data sample, for example into two parts: W=(ATBT)T, n=nA+nB.

Interesting examples of criteria in GMDH algorithms were proposed recently by:
  • Hild and Bozdogan define the ICOMP criteria [35] based on information-theoretical statistical theory, which take into account both parametric uncertainly as well as complexity, thereby eliminating the need for arbitrarily sub-dividing the data set for cross-validation;
  • Lange in [36] gives a review of selection criteria for the case of uncertainty;
  • Wang introduces the "Innovation-Contribution" criterion [37] in order to select independent variables automatically.