In discrete mathematics, the term template refers to a graph indicating which of the delayed arguments are used in setting up conditional and normal Gauss equations. A gradual increase in the structural complexity of candidate models corresponds to an increase in the complexity of templates whose explicit (a) and implicit (b) forms are shown: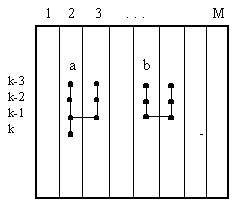

Implicit and explicit templates form

Figure: Derivation of conditional equations on a data sample.


The key feature of the algorithm is that it uses implicit templates, and an optimal model is therefore found as a system of algebraic or difference equations. Such system of models is received as result of consequent use of Combinatorial algorithm. The system criterion in OSA is a convolution of the criteria calculated by the equations that make up the system:

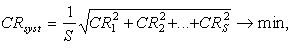
CRsyst = 1/S sqrt(CR1^2 + CR2^2 + ... +CRs^2)

where s is the number of equations in the system. The flowchart of the OSA algorithm is shown below.


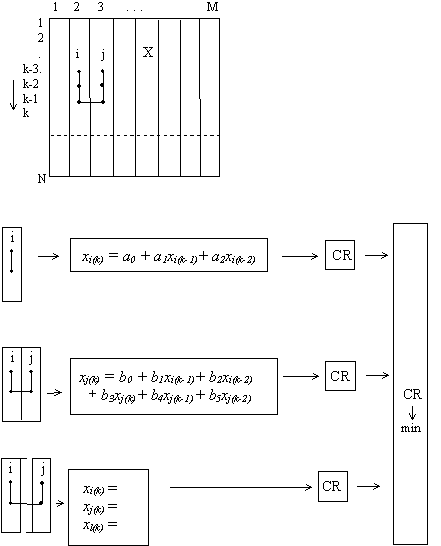
Objective System Analysis algorithm

An advantage of this algorithm is that the number of regressors is increased and in consequence, the information embedded in the data sample) is utilized better. It turns out that sorting-out by external criteria ensemble in OSA allow not only to choose the only optimal system of equations (in difference or algebraic form), but to show relations between elements of different complex objects, their effective input and output variables also.