Метод Группового Учета Аргументов применяется в самых различных областях для анализа данных и отыскания знаний, прогнозирования и моделирования систем, оптимизации и распознавания образов. Индуктивные алгоритмы МГУА дают уникальную возможность автоматически находить взаимозависимости в данных, выбрать оптимальную структуру модели или сети, и увеличить точность существующих алгоритмов.

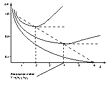Этот подход самоорганизации моделей принципиально отличается от обычно используемых дедуктивных методов. Он основан на индуктивных принципах - нахождение лучшего решения основано на переборе всевозможных вариантов.

При помощи перебора различных решений подход индуктивного моделирования пытается минимизировать роль предпосылок автора о результатах моделирования. Компьютер сам находит структуру модели и законы, действующие в объекте. Он может быть использован при создании искусственного интеллекта как советчик для разрешения споров и при принятии решений.

Метод Группового Учета Аргументов состоит из нескольких алгоритмов для решения разных задач. В него входят как параметрические, так и алгоритмы кластеризации, комплексирования аналогов, ребинаризации и вероятностные алгоритмы. Этот подход самоорганизации основан на переборе постепенно усложняющихся моделей и выборе наилучшего решения согласно минимуму внешнего критерия. В качестве базисных моделей используются не только полиномы но и также нелинейные, вероятностные функции или кластеризации.

Направление МГУА может быть полезным потому что:

• Находится оптимальная сложность структуры модели, адекватная уровню помех в выборке данных. (Для решения реальных проблем с зашумленными или короткими данными, упрощенные прогнозирующие модели оказываются более точными.)
• Количество слоев и нейронов в скрытых слоях, структура модели и другие оптимальные параметры нейросетей находятся автоматически.
• Гарантируется нахождение наиболее точной или несмещенной модели - метод не пропускает наилучшего решения во время перебора всех вариантов (в заданном классе функций)
• Любые нелинейные функции или признаки, которые могут иметь влияние на выходную переменную используются как входные аргументы
• Автоматически находит интерпретируемые взаимосвязи в данных и выбирает эффективные входные переменные
• Переборные алгоритмы МГУА довольно просто запрограмировать
• Метод использует информацию непосредственно из выборки данных и минимизирует влияние априорных предположений автора о результатах моделирования
• Подход МГУА используется для повышения точности других алгоритмов моделирования
• Дает возможность отыскания несмещенной физической модели объекта (закона или кластеризации) - одной и той же для всех будущих выборок.